有意差判定と誤差範囲（標本誤差≒許容誤差）
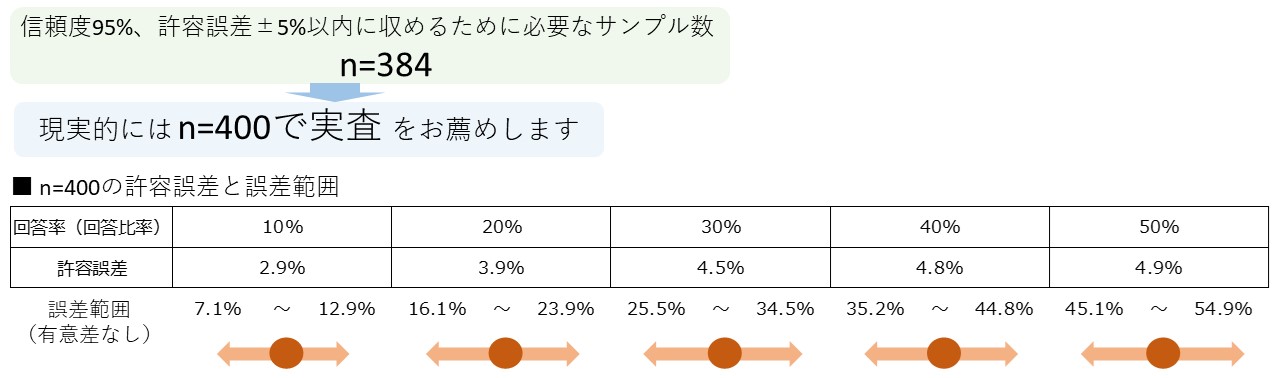
一般的な調査では、回答率の許容誤差を5％以内、且つ信頼度95％と設定し、400人のサンプル数での実施が目安となります。
（95％の確率で誤差が5％以内に収まる）
n=400の調査で、前回の認知率が30.0％の場合に今回の認知率が34.5％（+4.5pt）の場合はギリギリ誤差範囲内となります。よって有意差は認められません。
今回の認知率が34.6％（+4.6p以上）であればスコア上昇は有意である（有意差が見られる）、といえます。
下表を見ても分かる通り、 誤差（標本誤差≒誤差の最大値）は回答率が50％で最も大きくなります。
誤差（標本誤差）と必要サンプルサイズ
「標本誤差」とは、調査結果の回答率（％）の誤差範囲（最大の誤差値）のことです。
まずは調査のサンプルサイズ別に「最大の標本誤差」に大きな差があることを理解してください。
前回調査と今回調査の「認知率」の差、「購入意向」の差、「各イメージ項目回答率」の差などをイメージしてください。
この範囲内の差は、有意差が見られないことになります。
信頼度95％にて アンケートの回答率が50％（ｐ=0.5）とした場合、
サンプルサイズの違いによる最大誤差（誤差範囲）は以下のようになります。
サンプルサイズが10,000人であれば、ある質問に対する回答率が50%の場合、誤差は±1.0%となります。
母集団における誤差範囲内は49.0%～51.0%と推定できます。
⇒ 前回調査の認知率が50％で今回の認知率が51％（＋1.0pt）の場合は、認知率の上昇に有意差は見られません。しかし、今回の認知率が51.1％（＋1.1pt）であれば、認知率の上昇に有意差はあります。
サンプルサイズが100人だと誤差は10%近くになると考える必要があります。
⇒ 前回調査の認知率が50％で今回の認知率が60％（＋10.0pt）の場合は、認知率の上昇に有意差は見られません。しかし、今回の認知率が51.1％（＋1.1pt）であれば、認知率の上昇に有意差はあります。
許容誤差（希望する誤差の最大値）毎に必要となるサンプル数は異なります。
最大の誤差範囲を±5.0％と設定すると、調査に必要なサンプル数は384人≒400ssとなります。
しかし、±3.0％と設定すると1,067人≒1,000ssまたは1,100ssが必要となります。
誤差を半分にするためにはサンプルサイズを４倍にする必要があります。
400ssの調査は誤差範囲を考えるとコスパの良いサンプル数といえます。
必要サンプルサイズ計算式
許容できる誤差を設定した上でサンプルサイズを決める場合、たとえば信頼度95％（ｐ=0.5）として下の式を変換し、
で求めることができます。
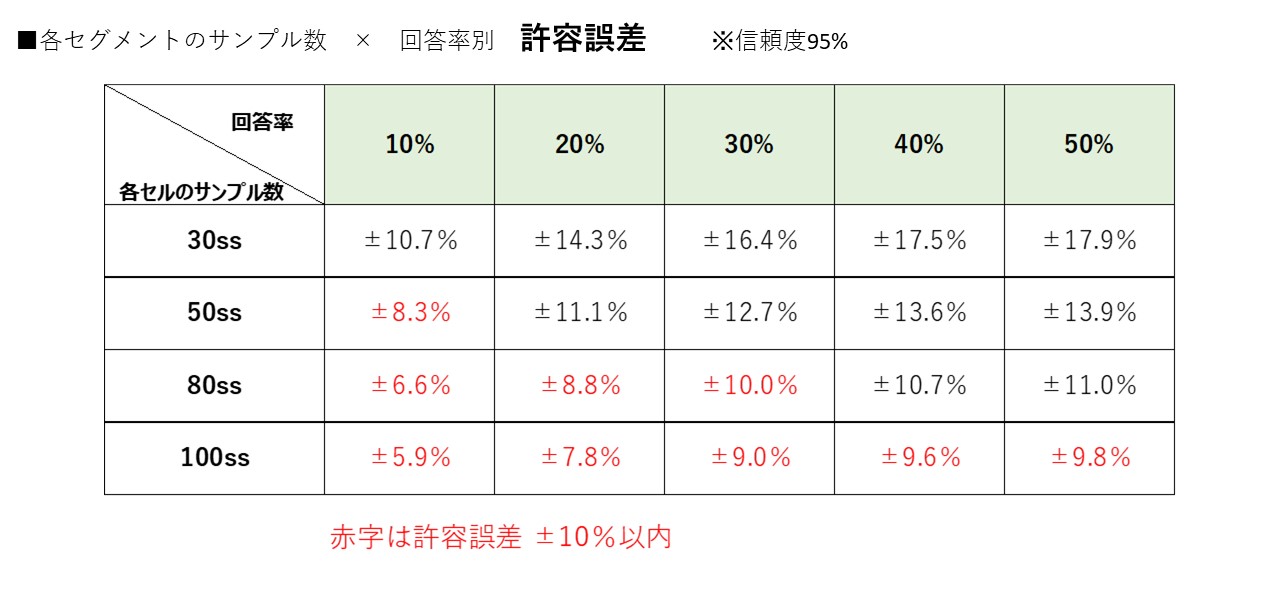
サンプルサイズ × 回答率別の誤差 （信頼度95％）
検定の数式は難解ですので、以下のシンプルな一覧表をご覧ください。
調査のサンプル数別に、設問の回答率別に、誤差の許容範囲が大きく異なることがわかります。
また、難しい？ｔ検定の分析や関数を用いなくても、有意差判定が可能です。
調査サンプル数を頭に入れて、回答率を確認して誤差の表をみれば有意なスコアが感覚的に理解できます。
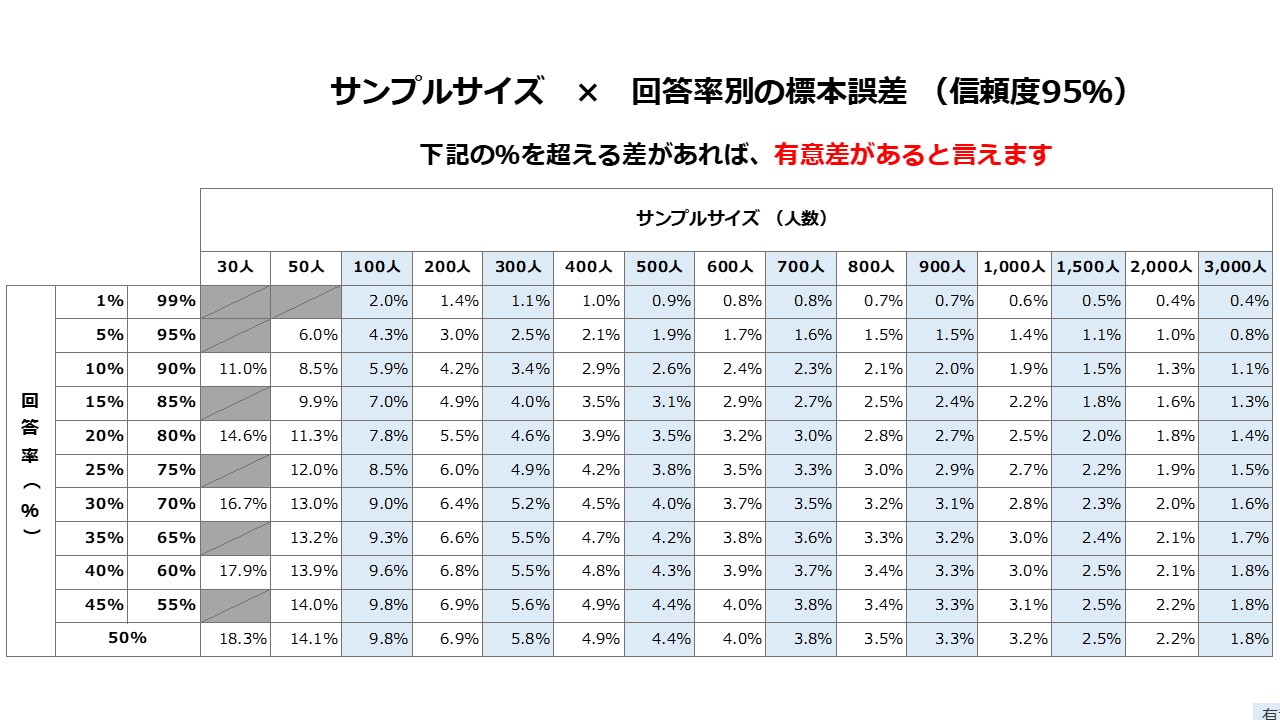
n=300の前回調査のイメージ項目『有名である』の回答率が１％で、今回調査で2.2％（+1.2pt）であれば、前回調査と有意差が見られる。と判断できます。
逆に、前回調査のイメージ項目『信頼できる』の回答率が40％で、今回調査で45.4％（+4.4pt）であっても有意差は見られません。
実際の分析での誤差の活用例 ⇒ 誤差表を使用した有意差検定
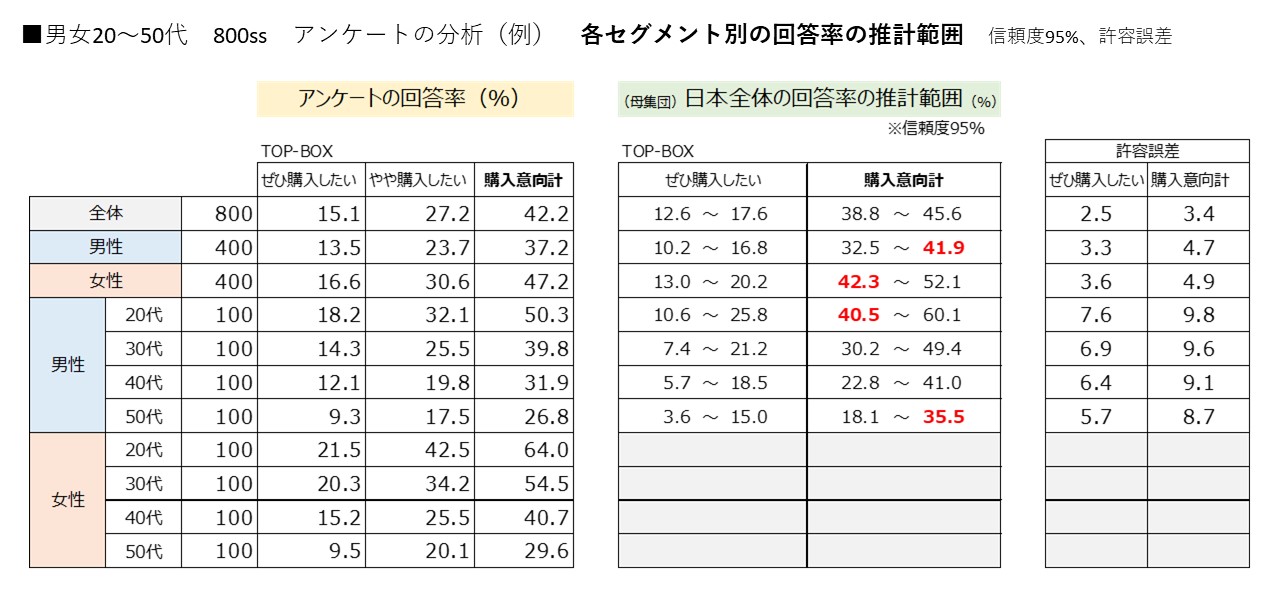
男女20～50代 800ss アンケートの分析（例） 各セグメント別の回答率の推計範囲を見てみましょう。
男性の購入意向率37.2％は、32.5％～41.9％の範囲に収まります。女性の購入意向率47.2％は42.3％～52.1％となり、
女性の下限値が男性の上限値を上回りますので、『極めて差が大きい』と言えます。
男性と女性の購入意向には有意な差が見られます。
男性の「ぜひ購入したい」13.5％、女性の16.6％と比較して、各誤差が±3.3～3.6％なので『やや差が見られる』と言えます。
男性と女性の購入意向top1「ぜひ購入したい」には有意な差が見られません。
性年代別はn=100となり有意差検定の精度が低くなりますので、「ぜひ購入したい」については男性20代（18.2％）と男性50代（9.3％）を比較して、やっと『やや差が見られる』と言えます。
男性20代の購入意向率50.3％、30代39.8％と比較して、各誤差が±8.7～9.8％なので『差が見られる』と言えます。
30代（39.8％）と40代（31.8％）を比較しても『やや差が見られる』と言えます。
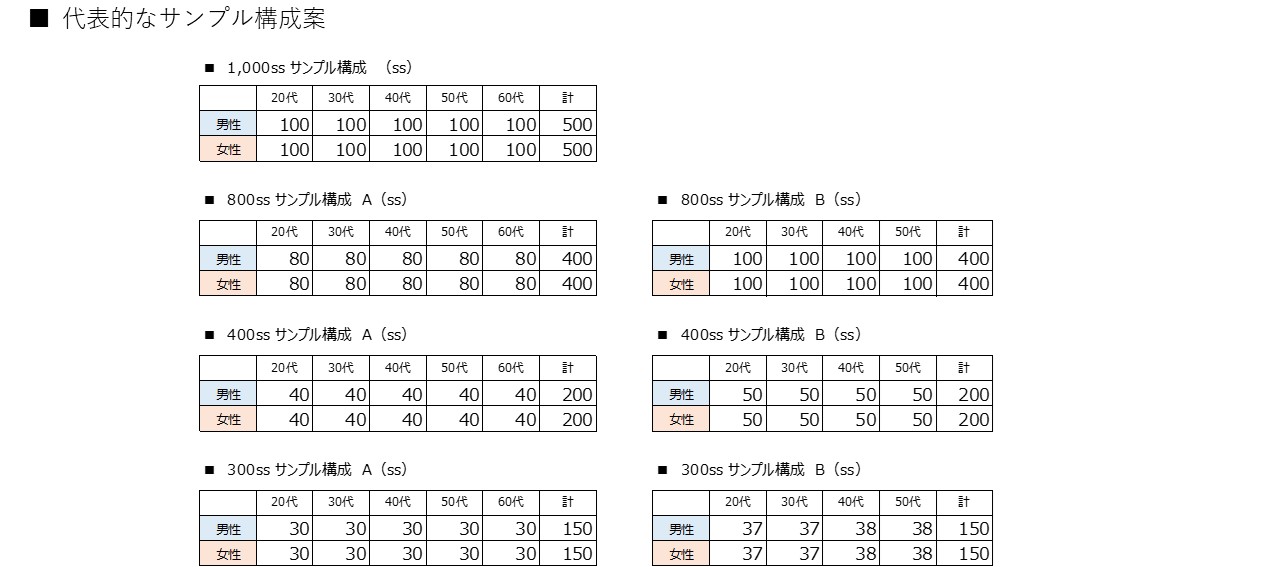
性年代別サンプル数の考え方① 男女別 『信頼度95％』
男女別に信頼度９５％、誤差±5％以内で比較、分析したい場合は男女各400s『計800ss』が必要となります。
→ 5％以上の差であれば男女別に差が見られる可能性が非常に高い。また2.5％以上差があれば、男女別に差が見られる可能性がある。と言えます。
予算の都合で？？男女各200s『計400ss』の場合の男女別でセグメントの誤差は±6.9％以内となります。
→ 7％以上の差であれば男女別に差が見られる可能性が非常に高い。また3.5％以上差があれば、男女別に差が見られる可能性がある。と言えます。
女性20～50代で10歳刻み各100s『計400ss』の場合は、各セグメントの誤差は±9.8％以内となります。
→ 10％以上の差であれば年代別に差が見られる可能性が非常に高い。また5％以上差があれば、年代別に差が見られる可能性がある。と言えます。
上記の誤差と解釈は、認知率・購入意向などの回答率が50％についてとなります。
回答率が10％であれば、誤差は概ね半分程度となります。
性年代別サンプル数の考え方② 男女10歳刻みで必要なサンプル数 『信頼度95％』
先ずは、一般的な男女年代別のサンプル数の割付を表示しました。
男女年代別のサンプル数30ss～100ssについて信頼度95％とした『サンプル数 × 誤差を一覧表』にしました。
回答率が10％と回答率50％で信頼できる回答率に大きな差があると同時に、やはり10代刻みのサンプル数は80ss以上欲しいと感じます。（理想論ですが）
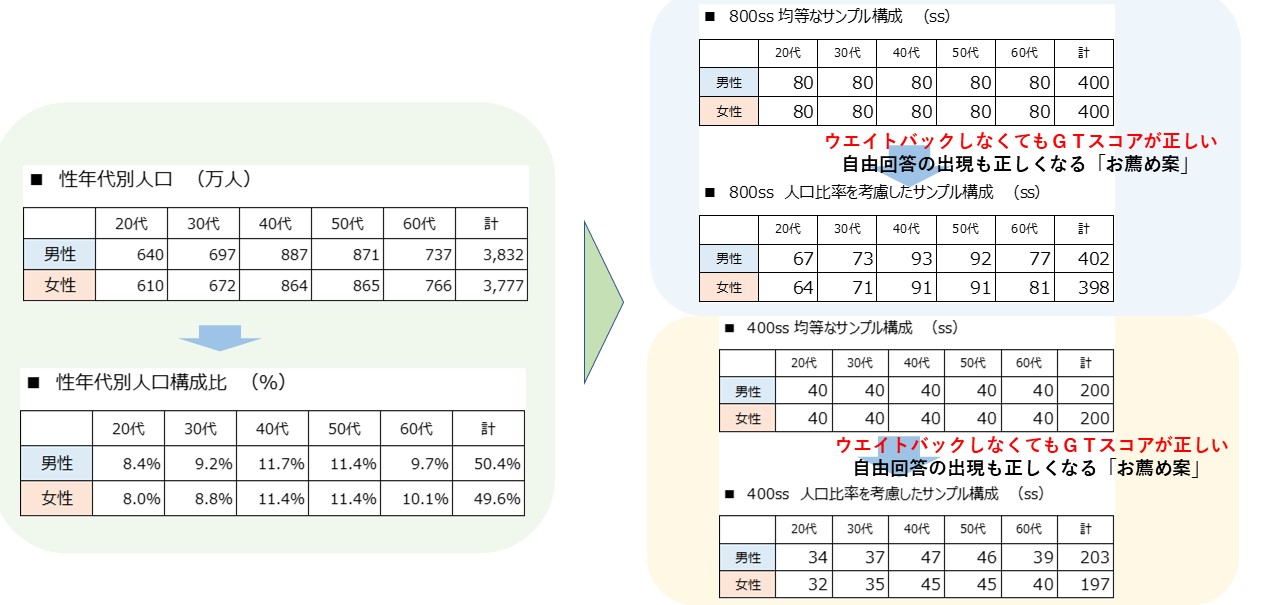
性年代別サンプル数の考え方③ 性年代別の人口を考慮 『信頼度95％』
先ずは左の日本の最新の性年代別の人口と構成比率をご覧ください。
次に、日本の最新の性年代別の人口を考慮して男女年代別に各セルを割付る案をご覧ください。
・ウエイトバックせずにＧＴのスコアが日本人全体の回答率に近似する優れものです。
・自由回答の出現率も正しくなる「お薦め案」です。
「誰にも聞けない有意差検定とモナ評価/コンペア評価の話」 → はこちら
サンプルサイズの自動計算サイト一覧
『誤差計算サイト』
「数学者|ビビッドアーミー考察・攻略」⇒画面下部にあります
「SurveyMonkey」⇒画面上部にあります
『母集団のサイズ（規模）の入力無し』
「ＦｒｅｅＡＳＹ」⇒画面上部にあります ※誤差の計算が可能で便利です
「GrooveWorks Inc.」⇒画面下部からエクセルをダウロードしてください
「ｋｅｉｓａｎ」⇒画面上部にあります
『定性調査』は定性調査の匠と職人の集まり ＳＡＲにお任せください！
■ＳＡＲの定性調査 以下のリンクをご覧ください
▼定性調査職人の集合体 ＳＡＲ
▼誰にも聞けないデプスインタビューのメリット
▼チャットGptによるデプスとグループインタビューの違い
▼ＳＡＲのインタビュー調査 最高レベルのスタッフとシステム
▼経営者に対しリモートインタビューが可能
▼理系大学生の採用に向けた調査／理系の転職採用インタビュー
▼食品調査の決定版 料理研究家ヒアリング調査『フードプロネット』
▼深掘り！日記調査システム『フォトインサイト』
▼最もコスパが良い組み合わせ『日記調査⇒対象者絞り込み⇒ＦＧＩ』はこちらをクリック
■ＳＡＲの定量調査 以下のリンクをご覧ください
▼ラダリング法の紹介『決定版』
▼経営者・意思決定者300名に対する定量調査
▼究極のパッケージ評価調査 パッケージの評価と改善策は
パッケージデザイナーに聞くのが一番
▼食品飲料の定量調査『フードプロネット』
■ＳＡＲの定性調査 以下のリンクをご覧ください ▼定性調査職人の集合体 ＳＡＲ
▼誰にも聞けないデプスインタビューのメリット ▼チャットGptによるデプスとグループインタビューの違い
▼ＳＡＲのインタビュー調査 最高レベルのスタッフとシステム ▼経営者に対しリモートインタビューが可能 ▼理系大学生の採用に向けた調査／理系の転職採用インタビュー ▼食品調査の決定版 料理研究家ヒアリング調査『フードプロネット』
▼深掘り！日記調査システム『フォトインサイト』 ▼最もコスパが良い組み合わせ『日記調査⇒対象者絞り込み⇒ＦＧＩ』はこちらをクリック
■ＳＡＲの定量調査 以下のリンクをご覧ください ▼ラダリング法の紹介『決定版』 ▼経営者・意思決定者300名に対する定量調査 ▼究極のパッケージ評価調査 パッケージの評価と改善策は パッケージデザイナーに聞くのが一番